The Monster Group: A Mathematical Analysis of Group Theory

- By Siddharth Velan

The monster group is also called the ‘friendly giant group’ and was constructed in 1982 by Robert Griess as a rotational group in an n - dimensional space.

We will come to what that number n is after a brief introduction.

Formally, a group is defined by taking a finite set and some operation or function that combines any two or more elements of the set to produce or replicate another third element of the same set, in such a way that the operation is valid for all properties such as associativity and the presence of an identity element. Every element must also have an inverse. In simpler terms, a mathematical group is an abstract set of numerals with operators added to it in such a way that all its identities are preserved. Geometrically, a group is arbitrarily defined as the possible conditions for symmetry or transformation- i.e. rotations, switching points, flipping etc.

Groups are fundamental in math and have other applications as well, such as the Poincare group (space-time relativity symmetry) and the Galois group (symmetry of the roots of a polynomial). Like these, many other groups are used for various purposes. The most basic fundamental groups, groups that cannot be divided into subgroups without any other function applied to it, such as integers.

Similarly, there are 18 countably infinite simple groups for which a pattern can be identified and applied. 26 other simple groups exist called sporadic groups and these are seemingly random with no identifiable system. The largest of all these so random groups is the monster group.

Coming back to the opening statement, a group can be applied to a number of dimensions, with a certain application for each. For any value of n, there is an n-dimensional representation of the group of order n! (n factorial), called ‘the natural permutation representation’. Our monster group is represented in a whopping 196883 dimensions.

The order of the gargantuan group is:

808,017,424,794,512,875,886,459,904,961,710,757,005,754,368,000,000,000 or

246 · 320 · 59 · 76 · 112 · 133 · 17 · 19 · 23 · 29 · 31 · 41 · 47 · 59 · 71,

which is a number unimaginable to us.

An element of this group would be represented as a matrix similar to this:

except there would be 196882 rows and 196882 columns. (excluding complex-dimension elements).

The monster group has a set of 20 sub-sporadic groups including itself, deemed ‘The Happy Family’ by Robert Griess. The other 6 were named ‘Pariahs’. Although renowned, the group doesn’t particularly represent anything.

Like geometric groups where you can visualize and apply the elements of the group, the monster group doesn’t have such pictorial representation. Fascinatingly, based on this, the monstrous moonshine conjecture was developed, establishing the unexpected connection between the monster group (M) and modular functions, in particular, the j function. The j function elicits elliptical structure along the complex plane, something outside the scope of this paper.

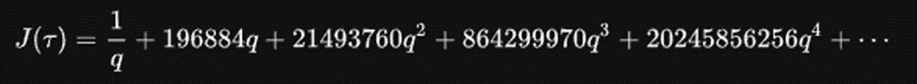
In this Fourier expansion of the j function, q=e^2πiτ ,

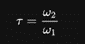
(half-period ratio of an elliptical function) the expression can be expressed in terms of the linear combinations of the dimensions of the irreducible representations,

Say r of the monster group (M) including a couple minute coefficients:

Let r equal 1, 196883, 21296876, 842609326, 18538750076, 19360062527, 293553734298, ... then

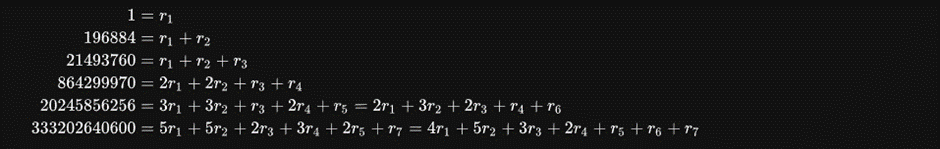
where the numbers on the left are the coefficients of the j function, while the ones on the right denote the dimensions, r , of the monster group (M). While such results are not coincidental, the exact relation between the monster group and other fields of physics is yet to be determined. Hence, while the monster is indeed unique and fascinating, the in-depth nature of it is incomprehensible to us as of now. What its applications can turn out to be is an event for the future.

References:

“Group theory, abstraction, and the 196883-dimensional monster” – 3Blue1Brown

Monster Group – Wikipedia

Monstrous Moonshine – Wikipedia

Monster Group – WolframMathworld

J-invariant – Wikipedia

Mathematical Group Theory – Wikipedia

The Friendly Giant – Robert Griess, 1982