Hidden Math Behind Art: The Fascinating Geometry of Tessellations

- By Lalitha Rao

Art and Math are two subjects that seem incredibly different, and while they may be in some aspects, they're in actuality, simultaneously similar. This review article is written in hopes of shining light on a form of art that relies on a fundamental understanding of geometry; Islamic Art.

The famous Agra Fort draws millions of tourists every year. One of the many gems of the monument is the intricate artwork. These geometric patterns are mostly seen in places of worship, the stunning patterns repeat almost infinitely, looming over wishful worshipers, thus creating a divine presence.

These masterpieces are created on the basis of tessellations. For instance, you may have made a checkered pattern with colored pieces of paper. This is nothing but a tessellation, wherein our tiles (squares of paper) form a repeating pattern covering the backing, clicking in perfectly with the next, consequently ensuring the absence of overlaps.

The above is what we call edge to edge tiling. Here, every edge of the square touches the next sharing the full side. The familiar “brick wall” is an example of non-edge to edge tiling, as one full side is not shared. There are several other forms of mathematical tiling, but most Islamic artwork employs the edge to edge form.

There are two types of tessellations: regular and semi-regular.

Regular designs are symmetrical, utilizing only one regular polygon, i.e, a shape in which all sides and angles are equal. For the sake of tessellations, art researchers have observed that only three shapes are able to form regular patterns. These shapes tessellate on their own and do not need others to fill in voids.

The needed shapes are an equilateral triangle, a square, and a hexagon. It is interesting that we see this in nature too, such as in a honeycomb or the outer layer of a pineapple, which are prominent examples of hexagonal tessellations.

For semi-regular tessellations, we look at shapes that cannot tessellate on their own and hence they are more of a collection of shapes. The regular pentagon is a prime example. A vertex is where the spades meet. The internal angles of a pentagon are 108. Mathematically, since this number is not a divisor of 360, there is a tessellation gap left. To resolve this, artists added other shapes such as a decagon and a hexagon and then tessellated this pattern.

In relation to tessellations, Islamic art is based on the divisions of a circle, there are several ways to divide a circle but most designs fall into one of the three categories.

1. Fourfold: these are patterns that can be based on the division of a circle into four equal sections.

2. Fivefold: these are patterns that can be based on the division of a circle into five equal sections.

3. Sixfold: these are patterns that can be based on the division of a circle into six equal sections.

Fourfold patterns fit into a square grid and hence they are fairly simple to tessellate. The same goes for sixfold, except they fit into a hexagonal grid. Fivefold patterns must be connected with other shapes to repeat, for the aforementioned reason that pentagons tesselate semi-regularly.

A recurring theme in all Islamic artwork (architecture included) is the use of a circle. To Muslims, this symbolizes the circle of unity. The center of this circle is symbolic of God and the city of Mecca. From this circle, several regular polygons can be developed by the intersection of lines stemming from the centre with the circumference.

What is so striking about this art form is the use of proportions, the ratios between the side lengths, and diagonals of regular polygons. These ratios are what make Islamic art so aesthetically pleasing and in the wise words of Aristotle- “maintain the just measure”.

Fourfold Patterns

Fourfold patterns are fairly simple and are created by connecting points of intersection to each other. In these types of patterns, the √2 proportion has been utilized. Moreover, the octagon, a shape associated with the eight directions of space and is a symbol of the divine throne, is derived from these divisions.

An example of a Moroccan tile using the Ocoton

Fivefold Patterns

With fivefold patterns we see the use of the golden ratio:

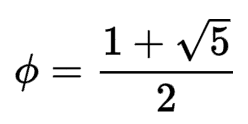
This is what makes the art near perfect.

Sixfold Patterns

Sixfold pattern

Sixfold patterns are very robust. They make use of the hexagon, a shape which can tesselate. The hexagon also contains √3 proportions and is a shape that resembles the Circle of Unity.

The shapes and number of divisions across all forms of Islamic art draw deep connections with the Islamic culture itself. This subject of geometry, although mathematical, is known as “Sacred Geometry”, as it connects art, math, and nature in these abstract ways that contort the mind, similar to the turning of a compass.

Now, I cannot finish this article without showing some of my creations. Here I have created a four-fold design. Looking at the template, there are several other patterns that can be created, but here I have focused on a design surrounding a square.

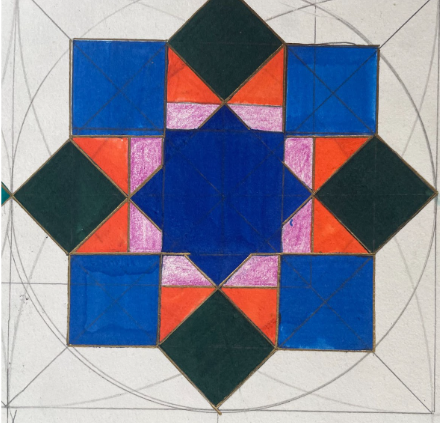
If this form of mathematical art intrigues you, and you want to dive deeper into its allure, the classical works of M.C Escher and Charles Gilchirst, which elucidate further on the interfaces between geometry and art, are immersive starting points. The story of tessellations profoundly used in Islamic art and architecture, is merely a small reflection of a much grander intersection between two disciplines that otherwise would be rendered disjoint and distinct. However, in the hopes that I have established this truth in this work, it can now be said that mathematics lives in art, and vice versa!