Arbitrary Rotated Ellipses: A Mathematical Mystery?

- By Rohan Joshi

I recently researched into quite an interesting way to find the equation of a rotated ellipse. An ellipse is characterized by the equation:

Where a is the length of the semi major axis and b is the length of the semi minor axis.

A rotated ellipse is exactly what it says, its appearance being self-explanatory:

In this article, I attempt to derive the formula for an arbitrary rotated ellipse: an ellipse with semi-major and semi-minor axes of lengths a and b rotated by an angle θ. What’s unique about this approach is that it looks at the ellipse from a 3-D point of view, while using concepts from simple harmonic motion.

Let’s take an arbitrary ellipse:

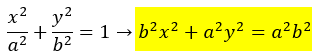
Observe the terms highlighted in yellow. This can be interpreted as the intersection of two 3-D graphs.

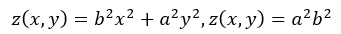
Now we do something unusual. We assume that the function z(x, y) describes the potential energy of an object. The force field associated with this potential is:

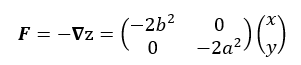
The eigenvalues of this matrix are -2b^2 and -2a^2 respectively. Their corresponding eigenvectors lie on the lines y=0 and x=0 respectively.

The force field above implies that if a particle is placed on one of the eigenvectors, then it undergoes simple harmonic motion. Therefore, simply rotating the potential energy graph will not change the nature of the motion, only the direction. So, even if the graph, and consequently the force field, are rotated by an angle θ, the eigenvalues will remain the same, while eigenvectors change. In fact, we can actually derive how this happens.

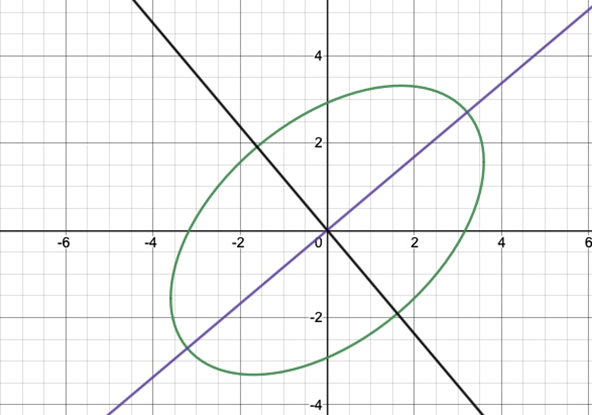
The rotated eigenvectors will be perpendicular, and it’s important to realize that the eigenvectors will be along the semi-major and semi-minor axes themselves. Thus, the lines containing the eigenvectors will becomes y=tanθx and y=-cotθx. The eigenvalues will remain the same (-2b^2 and -2a^2 respectively). The rotated z(x, y), which I’ll call z’(x, y), will represent a new force field F’.

Why have I assumed the components of the force field to be linear? Because the rotated graph is still a paraboloid, with quadratic terms. Differentiating the same, would provide an equation in linear terms.

The matrix in (1) will have the same eigenvalues mentioned before, but with different eigenvectors. Thus,

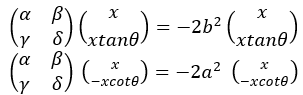
This will give us 4 equations in α, β, γ and δ.

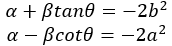
The solutions of these equations are:

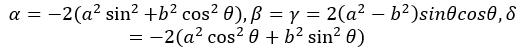
As expected, β=γ, as the field must be conservative. Then, we can use the facts

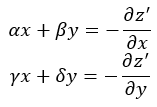
to derive z’. Thus,

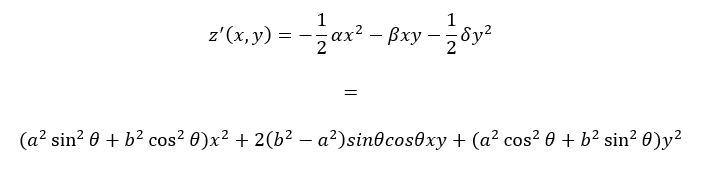
This is the function z’(x, y), which represents the rotated paraboloid curve.

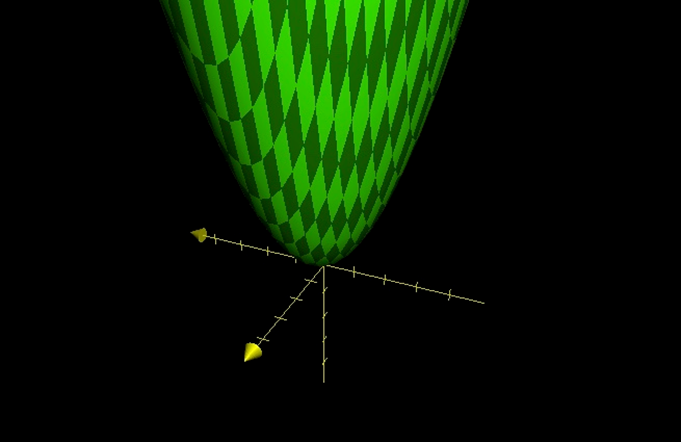
Now its important to realize that the graph above (z’(x, y)) is simply the original z(x, y) rotated. This means that we simply have to equate this function to z=a^2b^2 to find the equation for our rotated ellipse.

So, the equation of an ellipse rotated by an angle θ becomes:

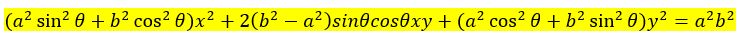
So that’s it! That’s the equation for an arbitrary rotated ellipse. The derivation is a little convoluted, but in the end, it leads to a rather fascinating and mathematically comprehensive result!