SIMPLE HARMONIC MOTION – PART 1

SIMPLE HARMONIC MOTION – PART 1

Look at the world around you. What do you see? Your room? Beautiful walls, plants of a magnificent verdant hue, a sparkly blue sky and birds chirping joyfully somewhere in the far distance? Or, if you live in a city, the hum of a drilling machine incessantly boring through some annoying neighbors flat at midnight, or the immense skyscrapers somewhere in the downtown. Right now, as I am typing this, I am pressing on the keys of my laptop, which promptly pop back up after I leave my fingers. What is common between all of these? Well, first, I shall apologize for that woeful image I presented. I am sure your surroundings are not as ideal as you’d like them to be, but, as an outside observer, I do have to make assumptions and approximations, do I not?

The simple harmonic oscillator is the most marvelous, and mystifyingly accurate approximation that describes this reality. All around us, the motion of everything in equilibrium, everything remotely periodic and even non-periodic, the motion of anything that transfers energy, is governed, at the simplest, molecular level, by the laws of simple harmonic motion. This article is just the first part of a many part journey into how oscillators work, and how they combine to transfer energy in the most wonderful of ways, and how the idea of an oscillator as the basis of reality arises most naturally from the dynamics of continuous media.

So, let’s start this exploration. In this article, I hope to cover the following:

1)    Hooke’s law

2)    A derivation of the trajectory of a particle attached to a spring, and

3)    A look at key concepts in SHM, such as frequency, time period, and amplitude

HOOKE’S LAW

Here’s the thing – no discussion about simple harmonic motion would be complete without Hooke’s law. Hooke’s law, simply put, governs the behavior of an ideal spring subjected to an external force. What is an ideal spring? Well, an ideal spring is massless and, um, obeys Hooke’s law. Put simply, the statement of Hooke’s law is this: the extension of an ideal spring under an applied force is directly proportional to the applied force, i.e.,

More rigorously, it is often written as:

Where k is the spring constant of the spring. This is nothing but a constant of proportionality. Now, consider the following situation: we have a mass m attached to an end of a string, and have applied a force F to extend it. What force does the spring exert on the mass? Since the mass is in equilibrium, this force must be equal and opposite to the applied force kx on the spring. Thus, for a mass connected to a spring, the force exerted by the spring is:

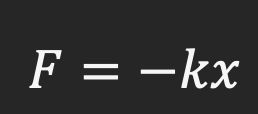
This is perhaps the most fundamental equation in all of classical mechanics. Now, what does a spring constant mean? Well, looking at the equations above, if the spring constant of a mass-spring system is high, it means that, for the same external force, the system would extend, or deform, to a smaller extent. Thus, the spring constant measures the rigidity of a spring. We will not get into matters of material science in this series, but the idea of a force being directly proportional to extension, connected by a constant, is something that simplifies the reaction of materials to external inputs. So, so, much.

Let us reflect, for a moment, that Hooke’s law is not just a mathematical statement, or even a fundamental theorem about the workings of reality. It is a statement of causality. It defines the idea of a spring constant, and by doing so it connects a measurable output, or extension, to some kind of measurable input, or force. Thus, in and of itself, Hooke’s law is a remarkable discovery that connects how matter deforms under inputs. With that, we come to the next important section of this article.

NEWTON’S LAWS AND THE MOTION OF A PARTICLE

We now have an expression for the force experienced by a particle on a spring. The next logical step here would be to derive an expression for the exact motion of the particle, as a function of time. How? Well, we can start with the other causal relation we know of: Newton’s second law, that the force on a particle is equal to its mass times its acceleration. For a particle on a spring in a vacuum, the net force will be the force exerted by the spring. Thus, we get:

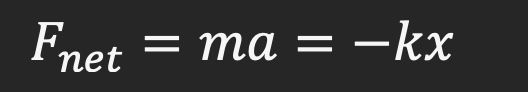
Then, realizing that acceleration is the second derivative of position,

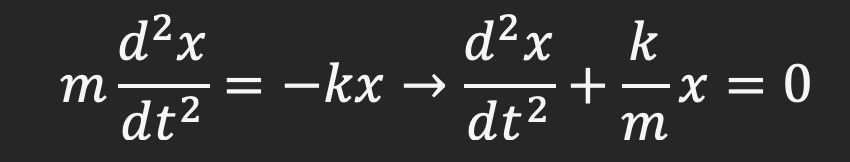
How do we solve this second order differential equation? Well, we assume the solution x(t) is of the form:

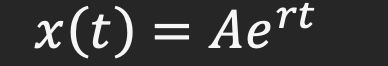
Substituting this into our equation and doing some calculus gives:

Thus, we have two options: either A is zero, which is a trivial solution (that would be the solution to any linear differential equation), or

Thus, we get:

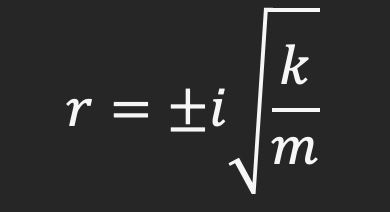
Note that we have two values of r, and thus our solution is a linear combination of both the possible solutions. Now, define:

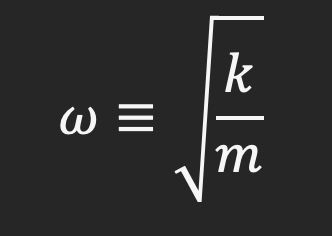
Thus, our general solution to the equation is:

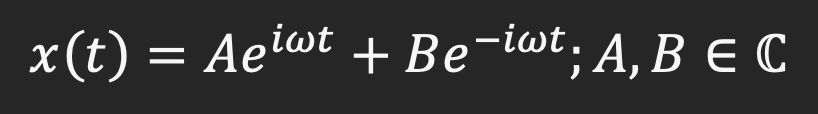
Well, the motion of particle is obviously real. We can actually simplify x(t) by writing it purely in terms of sines and cosines – an exercise left to the reader. Once the algebra is done, we get:

Thus, the motion of a particle on a spring is an oscillation back and forth about a mean position! Isn’t that wonderful? A graph is below, for reference:

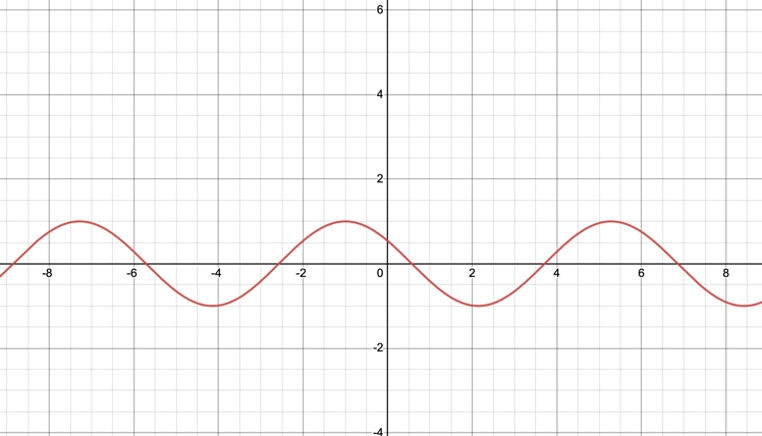
A graph of x(t), with A, ω, φ set to 1. Credit: Desmos

KEY CONCEPTS IN OSCILLATIONS

Now, we look at the expression for x(t) and see what is in it. The term A is known as the amplitude of the oscillation – it is the maximum displacement from the mean position. The quantity we defined as ω is the angular frequency of the oscillation. The time period of the oscillation is thus:

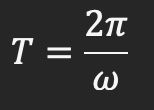
The factor of φ in the argument is the phase of the oscillator. This simply tells you at what point in the oscillation cycle the particle starts. It does not really matter when you want to analyse the motion of oneparticle. However, when you have multiple oscillations superposed on each other, these phases can interact with each other and affect the overall motion. What do I mean? We will come to that later.

For now, this introduction should be sufficient to set some of the mathematical background for the upcoming articles, as we will be diving into some beautiful mathematics. However, for now, I hope you understand the basics of simple harmonic motion, and the fundamental idea that, when a particle experiences a restoring force that is directly proportional to its displacement, the subsequent motion is always simple harmonic, and periodic. In the next article, we shall talk more about this, treating the system from the point of view of conservation of energy, and looking at damping as well. Till next time!