The Energetic Forces Behind Faraday's Law

-By Rohan Joshi

Image credit: Electromagnetic Energy Representation. https://taraenergy.com/blog/what-is-electromagnetic-energy-why-important/.

Picture this – you are in an electromagnetism class, let’s say this is middle school, and your teacher tells you, for the first time, that Faraday’s law is a thing – that a change in the magnetic flux through a region induces an electromotive force (well, voltage), across the wire/curve through which the field cuts to oppose the change in flux.

And this is an extremely powerful law – it is the basis of generators, of inductors, of the LC circuit, and had, at its first conception, astounding implications for the nature of the electromagnetic field. It seems a little counterintuitive, does it not? That the magnetic field can affect a change in the electric field? Well, I have found an intuitive explanation for this law. It is perhaps not the most mathematically or physically rigorous explanation, but to any of you who felt that this law seemed extremely arbitrary, founded entirely upon empirical evidence (not a bad thing, but knowing that some kind of theoretical background exists for a law always makes on feel better).

MAXWELL’S EQUATIONS

Now picture that you are in high school – or college, and your teacher, once again, tells you about Maxwell’s equations. Here they are, to jog your memory:

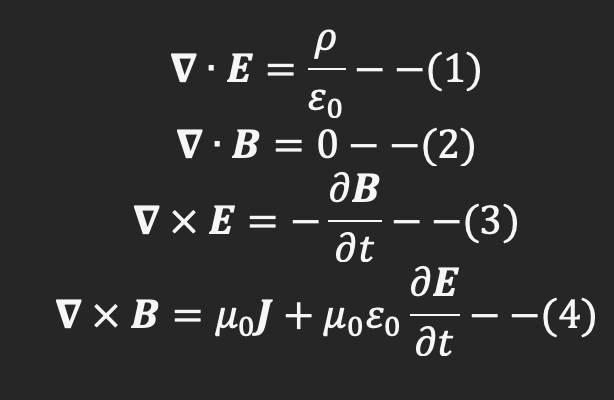
These equations specify the not just the nature of the electric and magnetic fields, but also their evolution through time. These equations are articulate, beautiful, as they also give us an idea as to how these fields are generated. The first one, Gauss’ law, tells us that an electric field is generated by a charge – we shall show that a varying electric field is actually equivalent to a current! Secondly, equations (4) says that magnetic fields are generated by moving charges – currents. Note the inclusion of the changing electric field. Lastly, the second one is simple – no magnetic monopoles exist.

The third one never really made sense to me – that is Faraday’s law, by the way. Or the Maxwell-Faraday law if you want to be pedantic. After all, (1) and (4) simply stated the origin of the electric and magnetic fields from their respective sources. Maybe (3) would make sense if magnetic “charges” existed, but (2) makes sure that this cannot happen. So, why, why does equation (3) make sense? Well, an explanation is coming up, and it involves perhaps the most important statement in all of physics – the conservation of energy.

BACKGROUND: RADIANT ENERGY

As we all know, electromagnetic energy travels in the form of waves – electric and magnetic fields oscillating at the speed of light through a vacuum, or any medium for that matter. However, these waves do not exist just for fun – they propagate energy through the medium. We will use this fact, along with the fact that electric and magnetic field oscillate perpendicular to each other, to demonstrate the nature of energy flow through a given region of space. The direction of propagation of these waves is that of the cross product of E and B. Now, consider a closed volume within space. The total energy E coming out of this volume will be proportional to the flux of the propagation vector through this region. Define F = k(E x B), where k is a scalar constant. Thus,

via the Divergence theorem. Now, if no energy is flowing out of a region of space, this tells us that

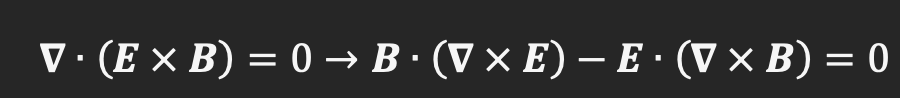
This is a fact that we will use later in the article.

ENERGY DENSITY

Another quick piece of background. The total energy density of the electromagnetic field in a vacuum is given by

The total energy of the field is thus

In the case that there is no outflow or inflow of energy,

CURRENT-FIELD EQUIVALENCE: A SLIGHT DETOUR

Last bit of background – once this is established, the explanation behind the third equation is pretty quick. Consider Ampere’s law:

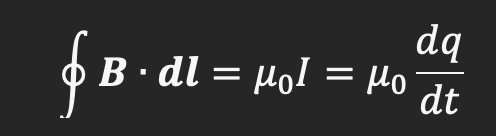
This tells us that a magnetic field B is created by a current. Now, the equivalence of current with a changing electric field can be shown in the case of a closed surface.

Thus, a time varying electric field in a close volume is equivalent to a current. Substituting the above into Ampere’s law in the absence of any “actual” current (the above quantity is called the displacement current), we get

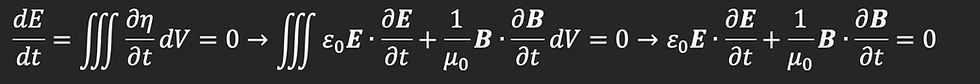
Which is equivalent to Maxwell’s fourth equation via Stoke’s theorem. Note that the surface integral has become open now in order to accommodate the formation of a magnetic field along any curve on the volume we are considering.

The concept behind Faraday’s law is a simple application of conservation of energy. We know from above that

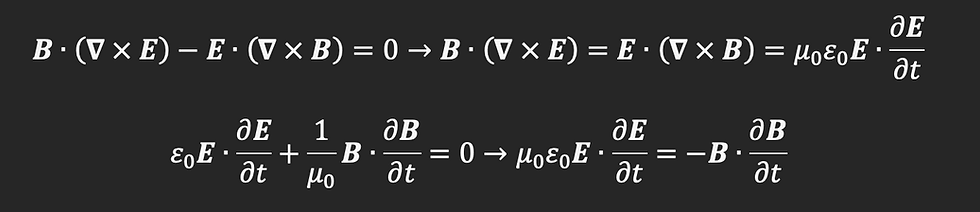
Thus,

And that is exactly equal to the third equation! Thus, through a simple application of the conservation of energy, we have proved that a time varying magnetic field produced an electric field! Physically, this can be thought of as follows. Consider a constant (in time) electromagnetic field existing in a given volume of space. Naturally, the total energy contained within this volume will be constant. However, if there is small “blip” in the magnetic field, that is, a small variation in time, the total energy of the volume changes. However, since this cannot happen, something else must happen to resist this change- the creation of a new electric field, whose curl is equal and opposite to the variation of the magnetic field with time!

There is also an interesting link between the creation of a “rotating” electric field, i.e., a field with a non-zero curl, and the equivalence between electric field and current we established. A time varying electric field will itself create a magnetic field, just like a current, to cancel out the “blip” in the existing magnetic field. Further, if there is actually a charge or wire present, the current induced will have the exact same effect!

So, that’s it! This may not be the most rigorous explanation, but this discovery provided me with a sense of closure – that Faraday’s law is not arbitrary. And I hope this article provides you with a deeper understanding of the same – that this law stems from the beautiful, infinitely elegant interplay that is the law of conservation of energy – that an induced electric field is simply a manifestation of energy being transferred from the magnetic field to an electric field/current.

CITATIONS:

Cadence System Analysis, et al. “The Energy Density of Electromagnetic Waves.” The Energy Density of Electromagnetic Waves, 13 Oct. 2022, resources.system-analysis.cadence.com/blog/msa2021-the-energy-density-of-electromagnetic-waves.